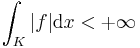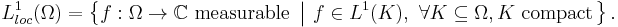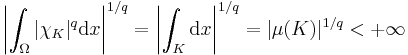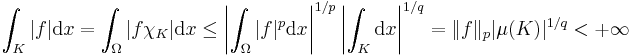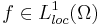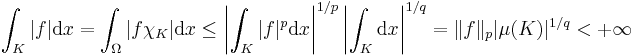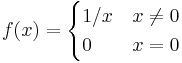Locally integrable function

In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.

1 Formal definition
2 Properties
3 Examples
4 Applications
5 See also
6 References
7 External links

Formal definition

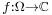Formally, let $\Omega$ be an open set in the Euclidean space ℝⁿ and $\scriptstyle f:\Omega\to\mathbb{C}$ be a Lebesgue measurable function. If the Lebesgue integral of $f$ is such that

$\int_K | f| \mathrm{d}x <%2B\infty\,$

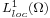i.e. it is finite for all compact subsets $K$ in $\Omega$ , then $f$ is called locally integrable. The set of all such functions is denoted by $\scriptstyle L^1_{loc}(\Omega)$ :

$L^1_{loc}(\Omega)=\left\{f:\Omega\to\mathbb{C}\text{ measurable }\left|\ f\in L^1(K),\ \forall K \subseteq \Omega, K \text{ compact}\right.\right\}.$

Properties

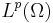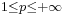Theorem. Every function $f$ belonging to $L^p(\Omega)$ , $\scriptstyle 1\leq p\leq%2B\infty$ , where $\Omega$ is an open subset of ℝⁿ is locally integrable.

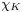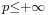
To see this, consider the characteristic function $\scriptstyle\chi_K$ of a compact subset $K$ of $\Omega$ : then, for $\scriptstyle p\leq%2B\infty$

$\left|{\int_\Omega|\chi_K|^q \mathrm{d}x}\right|^{1/q}=\left|{\int_K \mathrm{d}x}\right|^{1/q}=|\mu(K)|^{1/q}<%2B\infty$

where

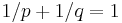$q$ is the positive number such that $1/p%2B1/q=1$ for a given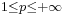 $\scriptstyle 1\leq p\leq%2B\infty$
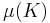$\mu(K)$ is the Lebesgue measure of the compact set $K$

Then by Hölder's inequality, the product 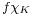$\scriptstyle f\chi_K$ is integrable i.e. belongs to 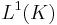$L^1(K)$ and

${\int_K|f|\mathrm{d}x}={\int_\Omega|f\chi_K|\mathrm{d}x}\leq\left|{\int_\Omega|f|^p\mathrm{d}x}\right|^{1/p}\left|{\int_K \mathrm{d}x}\right|^{1/q}=\|f\|_p|\mu(K)|^{1/q}<%2B\infty$

therefore

$f\in L^1_{loc}(\Omega)$

Note that since the following inequality is true

${\int_K|f|\mathrm{d}x}={\int_\Omega|f\chi_K|\mathrm{d}x}\leq\left|{\int_K|f|^p \mathrm{d}x}\right|^{1/p}\left|{\int_K \mathrm{d}x}\right|^{1/q}=\|f\|_p|\mu(K)|^{1/q}<%2B\infty$

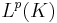the theorem is true also for functions $f$ belonging only to $L^p(K)$ for each compact subset $K$ of $\Omega$ .

Examples

The constant function 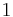$1$ defined on the real line is locally integrable but not globally integrable. More generally, continuous functions and constants are locally integrable.
The function

$f(x)= \begin{cases} 1/x &x\neq 0\\ 0 & x=0 \end{cases}$

is not locally integrable near $x=0$ .

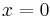Applications

Locally integrable functions play a prominent role in distribution theory. Also they occur in the definition of various classes of functions and function spaces, like functions of bounded variation.

References

Saks, Stanisław (1937), Theory of the Integral, Monografie Matematyczne, 7 (2nd ed.), Warszawa-Lwów: G.E. Stechert & Co., pp. VI+347, JFM 63.0183.05, MR 0167578, Zbl 0017.30004, http://matwbn.icm.edu.pl/kstresc.php?tom=7&wyd=10&jez=pl . English translation by Laurence Chisholm Young, with two additional notes by Stefan Banach: the Mathematical Reviews number refers to the Dover Publications 1964 edition, which is basically a reprint.
Strichartz, Robert S. (2003), A Guide to Distribution Theory and Fourier Transforms (2nd printing ed.), River Edge, NJ: World Scientific Publishers, pp. x+226, ISBN 981-238-430-8, MR 2000535, Zbl 1029.46039, http://books.google.it/books?id=T7vEOGGDCh4C&printsec=frontcover&dq=A+Guide+to+Distribution+Theory+and+Fourier+Transforms#v=onepage&q=&f=false .

External links

Rowland, Todd, "Locally integrable" from MathWorld.
Vinogradova, I.A. (2001), "Locally integrable function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=L/l060460

This article incorporates material from Locally integrable function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.